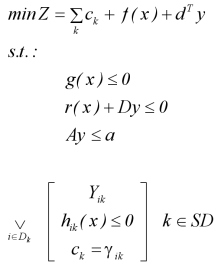
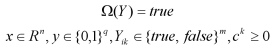
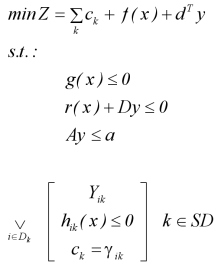
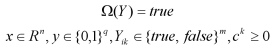
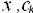 |
are continuous variables, |
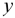 |
are binary variables (0-1), |
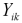 |
are Boolean variables, to establish whether a disjunction term is true or false |
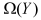 |
logic relationships between Boolean variables, |
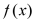 |
objective function, which can be linear or non-linear, |
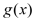 |
linear or non-linear inequalities independent of the discrete choices, |
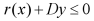 |
mixed-integer inequalities that can contain linear or non-linear continuous terms, |
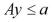 |
Integer inequalities |
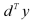 |
fixed cost terms. |