Language for the disjunction definitions: Definition Sentence

Definition of disjunctions with no domain

Consider the following two disjunctions:

The definition sentence consists of an IF..THEN..ELSE..ENDIF sentence. The syntax for a single disjunction is:

disjunction_name IS
IF term_condition THEN
  constraint_name_1;
  …
  constraint_name_i ;
  …
  constraint_name_n ;
[ELSE] | [ELSIF term_condition THEN]
  constraint_name_n+1;
  …
  constraint_name_r;
  …
  constraint_name_z;
ENDIF;

For the example presented we have two disjunctions that can be declared and defined as follows:

$ONECHO > "%lm.info%"
Disjunction D1, D2;
D1 IS
IF Y('1') THEN
   CONSTRAINT1;
   EQUATION1;
ELSIF Y('2') THEN
  CONSTRAINT2;
  EQUATION2;
ENDIF;<
D2 IS
IF Y('3') THEN
   CONSTRAINT3;
ELSE
   CONSTRAINT4;
ENDIF; $OFFECHO

Declaration and definition of CONSTRAINT1, CONSTRAINT2, CONSTRAINT3, CONSTRAINT4, EQUATION1 and EQUATION2 must be made in GAMS section of the input file.

Definition of disjunctions with domain

You can define a complete set of disjunctions over a given domain. Consider the following disjunction:

...which is defined over the domain j. The above represents j disjunctions (one for each value of the domain j) with two terms. Declaration and definition of the previous disjunction can be made as follows:

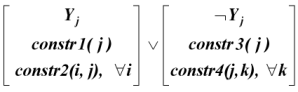
$ONECHO > "%lm.info%"
Disjunction D(j);
D(j) IS
IF Y(j) THEN
  CONSTR1(j);
  CONSTR2(i,j);
ELSE
  CONSTR3(j);
  CONSTR4(j,k);
ENDIF;
$OFFECHO

Where i,k, j are SETs defined in GAMS section. Suppose the following definitions in GAMS section:
SET i /1*3/, k /a,b/, j/1*2/
The previous disjunction definition is equivalent to:

$ONECHO > "%lm.info%"
Disjunction D(j);
D('1') IS
IF Y('1') THEN
  CONSTR1('1');
  CONSTR2('1','1');
  CONSTR2('2','1');
  CONSTR2('3','1');
ELSE
  CONSTR3('1');
  CONSTR4('1','a');
  CONSTR4('1','b');
ENDIF;

D('2') IS
IF Y('2') THEN
  CONSTR1('2');
  CONSTR2('1','2');
  CONSTR2('2','2');
  CONSTR2('3','2');
ELSE
  CONSTR3('2');
  CONSTR4('2','a');
  CONSTR4('2','b');
ENDIF;
$OFFECHO

From the previous definition, since j has two elements, only two disjunctions correspond to the domain.
Both definitions presented above are equivalent and valid for the LOGMIP compiler.

Definition of disjunctions with restricted domain

The constraint and disjunction’s domain can be controlled by thesentence with in conjunction with other operators:

Relational operators:

lt,<	: less than
le, <=	: less than or equal to
eq, =	: equal
gt, >	: greater than
ge, <=	: greater than or equal to

Sets operators:

ord	: order of an item in the set
card	: number of items in the set
in	: inclusion of a set item

Logic operators: and, or.

Using subsets

If you have defined a disjunction over a domain and you have also the disjunction’s variables and constraints defined over the same or different domain, you can have two situations, which are:

constraints and variables whose domain is under the control of the disjunction domain.
constraints and variables with uncontrolled domains, which must be defined in order to avoid semantic errors.

If you need to control a set domain that is already controlled by the disjunction definition, you must use an ALIAS for that set and redefinethe domain over that ALIAS. See example 3 for this purpose.
Some illustrative examples are presented with the intention of clarifying these matters.

Example 1: using with, ord and card to controlling disjunction domains
Example 2: using with and ord clause to controlling disjunction domains and constraints domain
Example 3: using with and ord clause to controlling disjunction domains and domains that are already controlled
Example 4: Using a subset and the GAMS GDX facilities
Example 5: A larger example using SUBSETS
Example 6: Using the operator IN